홀수 절점 제거 개념의 상수 공급 관망 설계 적용에 관한 타당성 연구
A Feasibility Study on Applying the Concept of Removing Odd Nodes to Design of Water Supply Pipe Network
Article information
Abstract
목적
본 연구에서는 블록시스템의 단점인 과다한 절점 및 관로의 복잡성으로 인해 발생하는 손실 수두와 잔류 염소의 급격한 감소 문제를 해결할 수 있는 방안으로, 이미 제시된 Eulerian path개념과 본 연구에서 새롭게 제안하고자 하는 non-Euerian path 개념을 비교하고 검토하고자 한다.
방법
‘홀수 절점 제거’, ‘3교차점 연결관로 제거’, ‘수요량 없는 절점 제거’ 개념을 가상 관망에 적용하여 경우의 수를 분석하고 각 시나리오별로 구성 및 수리 관점에서 평가하여 가장 효율적인 방안을 제시하였다. Euler 그래프와 non-Euler 그래프 상수 관망을 대상으로 EPANET2로 각 총관로길이, 제거 관로수, 압력수두 및 유량을 모사· 비교하였다.
결과 및 토의
가상 Euler 및 non-Euler 그래프 상수관망을 대상으로 절점을 제거하고 새로운 관망을 구성한 결과 3교차점 연결관로 제거 개념이 보다 많은 관로를 제거함으로써 효율을 높일 수 있을 것으로 확인되었다. 그러나 홀수 절점 연결관로 제거 개념은 상수 관망을 Euler 그래프로 형성함으로써 보다 합리적인 상수관망 설계 및 운영 기법을 제시하는 것으로 판단된다.
결과 및 토의
상수 관망을 완벽한 Euler 그래프로 구성하는 것은 무리가 있다. 이에 본 연구에서 제시하는 홀수 절점 연결 관로 제거 개념의 적용은 효율적인 상수관망의 단순화를 도모할 수 있다. 또한 이 개념의 적용은 수리 및 수질적 관점에서 효율을 기대할 수 있을 것으로 사료된다.
Trans Abstract
Objectives
In this study, the concept of the Eulerian path, which has already been proposed as a solution to the problem of head loss and residual chlorine reduction caused by complexity of nodes and pipelines, and the non-Euerian path proposed in this study were compared and their feasibility were examined.
Methods
The concepts of ‘removal of odd nodes’, ‘removal of 3-intersection nodes’, and ‘removal of zero demand nodes’ were applied to the virtual water supply networks, and the number of cases were analyzed and evaluated from the viewpoint of configuration complexity and hydraulic efficiency. For Euler graph and non-Euler graph water supply networks, each total pipe length, number of removal pipes, pressure head and flow rate were simulated with EPANET2 program.
Results and Discussion
As a result of simplifying and designing new output networks for virtual Euler and non-Euler graph, it was revealed that the concept of ‘removing a 3-intersection nodes’ could be the most efficient by removing more pipes. However, in terms of configuring the output network as an Euler graph, the concept of ‘removing odd nodes’ can be considered more reasonable.
Conclusion
It is difficult to configuring watersupply network as a perfect Euler graph. Therefore, the application of the concept of removing odd nodes suggested in this study can promote efficient simplification of the network. In addition, it can be thought that the application of this concept can expect efficiency in terms of hydraulics and water quality.
1. 서 론
전통적인 상수 관망의 계획 및 설계는 도시계획을 근간으로 주요 도로를 통과하는 배수관로와 배수관로로부터 수용가까지를 연결하는 급수관로로 구성되어 있다. 상수 관망의 계획 및 설계에 있어서는 수량 공급의 안정성, 수압 유지의 적정성 및 수질 보전 기능을 고려하여 엔지니어의 공학적인 판단으로 관로의 노선, 관경 및 연결상태가 결정된다[1]. 대부분 도시의 경우 산업화 및 도시화로 인한 급격한 팽창이 이루어져 기존의 상수 관망에 신설 관망을 중복하여 설치하거나 노후 상수도관 개량사업을 통해 관로를 개량 또는 확장하는 경우 실제 관망의 기능을 유지하기 위하여 필수적인 관로 이외 많은 불필요한 관로가 설치, 운영된다[2]. 특히 상수 관망은 지하에 매설되어 확인이 불가능한 경우가 많아 불필요한 관로에서 발생되는 누수와 수질의 악화 등 운영관리에 부정적인 영향을 미친다.
Yoon 등은 ‘Eulerian path’개념을 상수 관망 설계에 적용하여 무의미관 및 불필요한 관로를 제거할 수 있는 기법을 제시하고 그 타당성을 입증하였다[2]. 그들은 경제성 분석을 통하여 상수 관망의 계획 및 설계 단계에서 불필요한 관로의 제거는 공사비를 절감할 수 있는 효과를 발생시키며, 운영 및 유지관리 단계에서 불필요한 관로의 제거는 운영관리의 최적화 및 수질을 보전하는 데에 긍정적인 효과를 나타냄을 보여주었다. ‘Eulerian path’ 개념은 ‘그래프(graph)의 모든 변(edge)을 중복하지 않고 지나가는 경로’ 정의되며, C-language를 이용하여 상수 관망의 계획 및 설계, 운영 및 유지관리에 적용할 수 있는 프로그램도 제시하였다. 그런데 Eulerian path가 실제 운영 중인 상수관망에서 무의미관이나 불필요한 관을 제거하는 데에 적용되는 경우 수리 및 수질의 해석 및 평가가 실시간으로 가능한지 검증이 완전하지 않았다. Eulerian path 개념을 이용하여 불필요한 관을 제거하는 경우 절점(수용가)에 충분한 용수가 적정한 압력으로 공급되는지 또는 취수원으로부터 절점(수용가)까지 수돗물의 공급과정에서 적정한 농도의 잔류염소가 유지되는지가 설계자 및 운영자의 가장 큰 관심 사항이다.
상수 관망은 크게 수지형(tree type)과 블록형(block type)으로 구분된다. 수지형 관로에 비해 블록형 시스템의 구축은 유량계, 수압계, 수질모니터링센서 등의 감시장비와 감압밸브 같은 제어시설을 효과적으로 설치, 운영하는 것에 의해서 더욱 안정적이고 효율적인 관리가 가능하게 된다. 특히 관로의 개량 및 교체, 누수복구, 야간최소유량조사, 관 세척작업과 같이 단수가 필요한 유지관리 업무를 수행하는데 있어 보다 신속하고 정확한 업무처리가 가능하게 되는 등 많은 장점이 있다[3~6]. 그러나 블록시스템을 도입한 해외 도시에서는 관망의 유지관리의 복잡성, 상수 수요 변동 및 대형 사고에 대한 탄력성 부족, 관내 체류시간 장기화와 관내 유속 저하로 발생하는 2차 오염(잔류염소 농도 저하와 생물막 오염 등), 높은 초기 투자비 및 운영관리비 및 무의미관(meaningless pipe)의 생성 등 단점 또한 지속적으로 제기되어 온 바이다[7]. Jafari 등은 블록형 상수 관망에 대해 과도한 손실 수두를 극복하고 용수를 공급하기 위해 발생하는 수요 지점별 압력 편차로 누수의 증가를 문제 삼았다[8].
이에 본 연구에서는 블록시스템의 단점인 과다한 절점 및 관로의 복잡성으로 인해 발생하는 손실 수두와 잔류 염소의 급격한 감소 문제를 해결할 수 있는 방안으로 기 제시된 Eulerian path개념과 Euerian path 개념과 상관없이 불필요한 관로를 제거할 수 있는 개념의 적용 타당성을 본 논문에서 제시하고자 한다. 관망 전체를 완벽한 Eulerian path 개념을 적용하는 것이 아니라 부분적으로 Non-Eulerian path 개념을 적용한 ‘홀수 절점 제거’, ‘3교차점 연결관로 제거’, ‘수요량 없는 절점 제거’ 개념을 작위의 관망에 적용하여 경우의 수를 분석하고 각 시나리오별로 구성 및 수리학 관점에서 평가하여 가장 효율적인 방안을 제시하고자 한다. ‘홀수 절점 제거’ 및 ‘3교차점 연결관로 제거’ 개념은 Eulerian path 개념에서 파생되었지만 전체 관망을 대상으로 ‘한 붓 그리기’를 할 수 없다는 관점에서 Non-Eulerian path 개념(부분적인 Eulerian path)에 포함시키고자 한다.
2. Eulerian path와 Non-Eulerian path의 개념 설명
2.1. Eulerian path 개념
한 번 지나간 선으로는 지나가지 않고 모든 선을 이어 그림을 완성하는 것을 우리는 한붓그리기로 정의한다. 붓을 종이에서 떼지 않고 한 번에 그린다고 해서 명명되었다. 이산수학에서는 시작점과 끝나는 점이 동일한 경우를 ‘Eulerian Circuit’ 이라 정의하고 시작점과 끝나는 점이 동일하지 않은 경우를 ‘Eulerian Trail’로 정의한다. Fig. 1에서 나타낸 바와 같이 우체부가 쾨니히스베르크에 있는 7개의 다리(변)를 단 한 번씩만 건너서 다시 출발점으로 되돌아 올 수 있는가의 문제를 1736년에 레온하르트 오일러가 그런 방법은 없다고 증명한 것을 Eulerina path의 이론적 출발점으로 보고 있다[9~11].
임의의 도형에서 Eulerian circuit이 존재하는 조건은 절점의 차수(절점에 모이는 변의 개수)가 모두 짝수인 경우이다(Fig. 2(a). 이 조건에서는 어떤 점에서 출발해도 다시 출발점으로 되돌아 올수 있다. 또한 Eulerian trail이 존재하는 경우(Fig. 2(b)) 차수가 홀수점에서 출발하면 다른 홀수 차수점으로 도착하게 된다. 이러한 경우 Eulerian trail은 존재하지만 Eulerian circuit은 존재하지 않게 된다. 그 이외에 홀수점이 2개가 넘는 경우나 1개가 되는 경우에는 한붓그리기가 불가능하다.
2.2. 홀수 절점 연결관로 제거 개념
본 개념은 홀수 절점 연결관로를 제거함으로써 상수관망의 그래프를 오일러 그래프(Euler graph)에 근접한 배치(layout)가 되도록 하는 것이다. 본 개념에서는 먼저 절점(node)에 연결된 관로(변, edge)의 수가 ‘3개 이상의 홀수’ 조합인 경우에 해당하는 절점을 선택한다. 그리고 해당 홀수 절점에 연결된 관로를 순차적으로 제거하면서 평가한다. 평가 시 관로에 연결된 다른 절점이 3개 이상의 홀수 관로와 연결되어 있고 해당 관로의 양 절점으로부터 취수원(저수지, reservoir)까지의 경로가 존재하는 경우, Euler 경로 구성 조합에 추가한다.
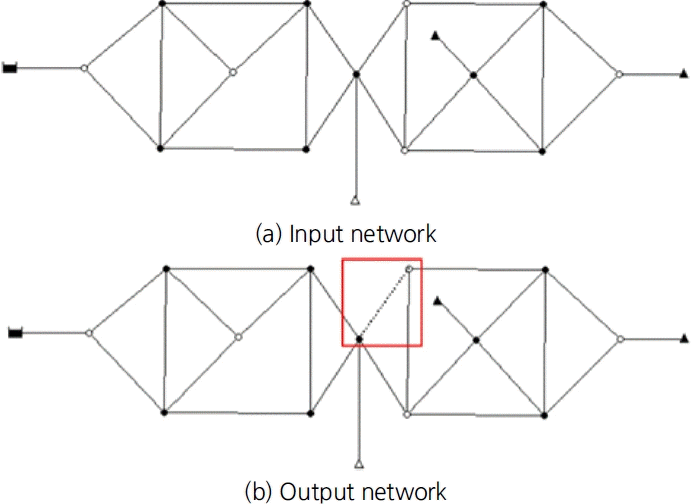
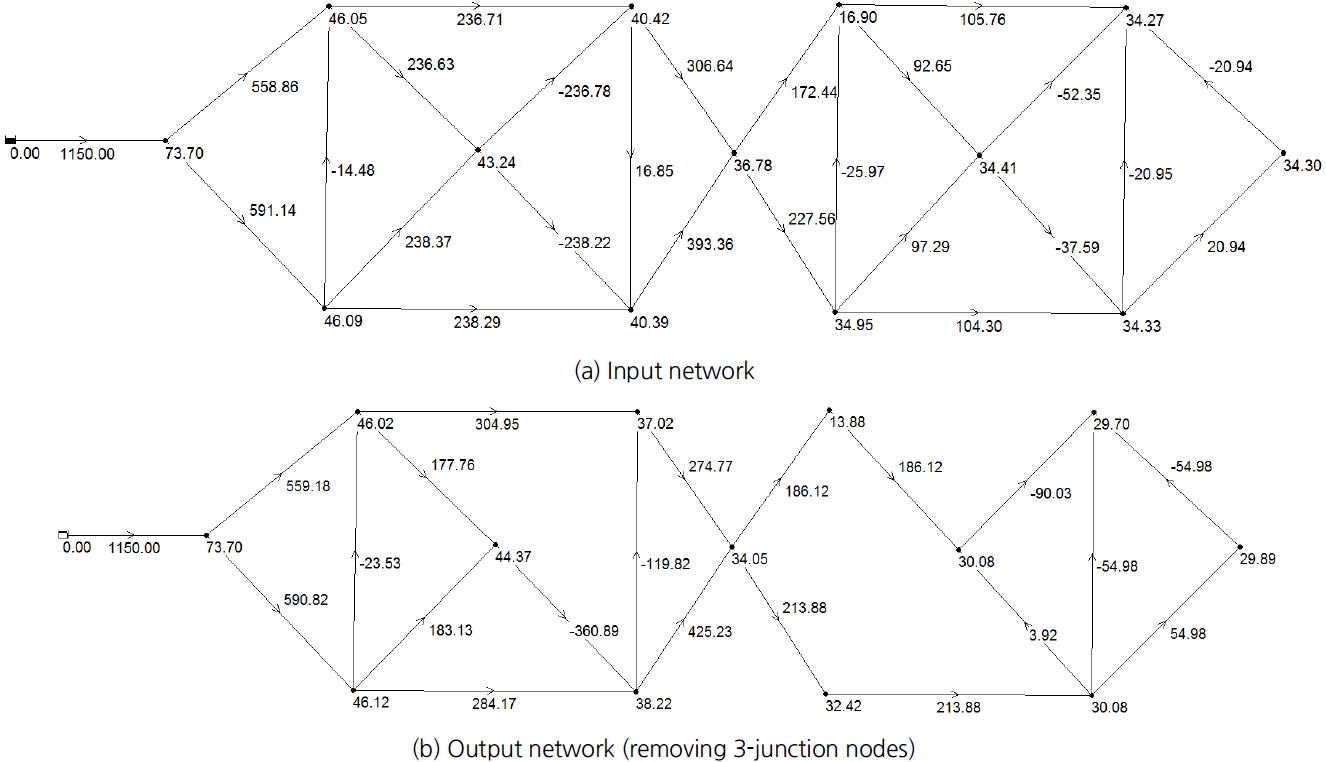
Fig. 3은 본 연구를 위해 가상으로 만든 입력관로(input network)와 홀수 절점 연결관로를 제거한 출력관로(output network)의 조합 중 하나를 나타낸 것이다. 빨간 윤곽선 박스의 그래프를 살펴보면 다른 관로들과 달리 점선으로 표시된 관로가 제거 대상 관로이다. 점선 관로를 제거하는 경우 왼쪽 다섯 개의 관로 절점은 네 개로, 오른쪽 세 개의 관로 절점은 두 개로 변환된다. 즉, 홀수 절점 연결관로 제거 개념을 통해 불필요한 관로의 제거가 가능함을 알 수 있다.
2.3. 3교차점 연결관로 제거 개념
본 개념은 절점 연결관로를 가능한 많이 제거함으로써 불필요한 관로 제거효율을 최대한 높일 수 있으며, 상수 관망의 그래프는 Euler 그래프의 배치와는 관련이 없다. 본 개념에서는 먼저 절점에 연결된 관로의 수가 3개 이상의 조합인 경우에 해당되는 절점을 선택한다. 그리고 해당 홀수 절점에 연결된 관로를 순차적으로 제거 평가해간다. 이 과정에서 관로에 연결된 다른 절점이 3개 이상 관로와 연결되어 있고, 해당 관로의 양 절점으로부터 취수원(저수지)까지의 경로가 존재하는 경우, non-Euler 경로 구성 조합에 추가한다.
Fig. 4는 본 연구의 대상인 입력 관로로부터 3교차점 연결관로를 제거한 출력관로 조합 중 하나를 나타내고 있다. 3개의 빨간 윤곽선 박스 내의 그래프를 살펴보면 다른 관로들과는 달리 점선으로 표시되어 있다. 즉, 3교차점 연결관로 제거의 알고리즘을 통해 불필요한 관로가 제거될 수 있음을 알 수 있다. ‘2.2 홀수 절점 연결관로 제거’ 개념에서는 1개의 관로만이 제거된 것과 비교하여 본 3교차점 연결관로 제거는 3개의 관로가 제거될 수 있었다. 단 복잡한 관로를 단순화하는데 효과적일 수 있지만 용수공급의 신뢰성은 평가가 필요하다.
2.4. 수요량 없는 절점 제거 개념
본 개념은 앞서 언급한 홀수 절점 연결관로 제거 개념과 3교차점 연결관로 제거 개념을 적용한 후 추가적으로 불필요한 관로 및 절점을 제거할 필요가 있는 경우 적용을 검토하는 방법이다. 또한 홀수 절점 연결관로 제거 개념과 3교차점 연결관로 제거 개념 적용 없이 용수 수요량이 없는 관로와 절점 제거에도 적용 가능하다. 본 개념에서는 용수 수요량이 없는 절점을 찾아 절점에서 연결된 관로가 한 개인 경우 해당 절점과 관로의 제거를 평가한다. 특히, 본 개념은 홀수 절점 연결관로 제거 개념과 3교차점 연결관로 제거 개념을 적용한 후 많은 상수관망의 조합 중 하나를 선택하여 수요량이 없는 절점을 제거할 때 효율을 최대로 높일 수 있을 것으로 예측하였다.
Fig. 5는 입력 관로로부터 수요량이 없는 절점을 제거한 출력 관로를 예시하고 있다. 입력 관로의 빨간 윤곽선 내의 그래프를 살펴보면 관말의 절점이 △로 표기되어 있음을 알 수 있다. 해당 절점은 용수 수요량이 없고 하나의 관로와 연결된 상태이다. 이에 용수 수요량이 없는 절점과 관로를 제거함으로써 상수관망 운영상 발생할 수 있는 누수 가능성을 줄일 수 있는 것으로 기대하였다. 그러나 본 연구에서는 수요량이 없는 절점의 효과를 검증하지는 않았다.
3. 연구방법
3.1. 연구 대상 관로의 특성
Euler 그래프는 모든 변을 중복 없이 포함하는 그래프를 의미한다. Euler 그래프가 성립되기 위한 두 가지 조건은 먼저 모든 꼭짓점의 차수가 짝수이거나, 홀수 차수 꼭짓점의 수가 ‘2’가 되어야 한다. 모든 꼭짓점의 차수가 짝수인 경우에는 Euler 그래프의 시작점과 끝점이 같은 폐쇄경로를 형성하며, 홀수 차수 꼭짓점의 수가 ‘2’인 경우에는 홀수 꼭짓점으로부터 시작된 경로는 다른 홀수 꼭짓점에서 끝나는 열린 경로를 형성한다.
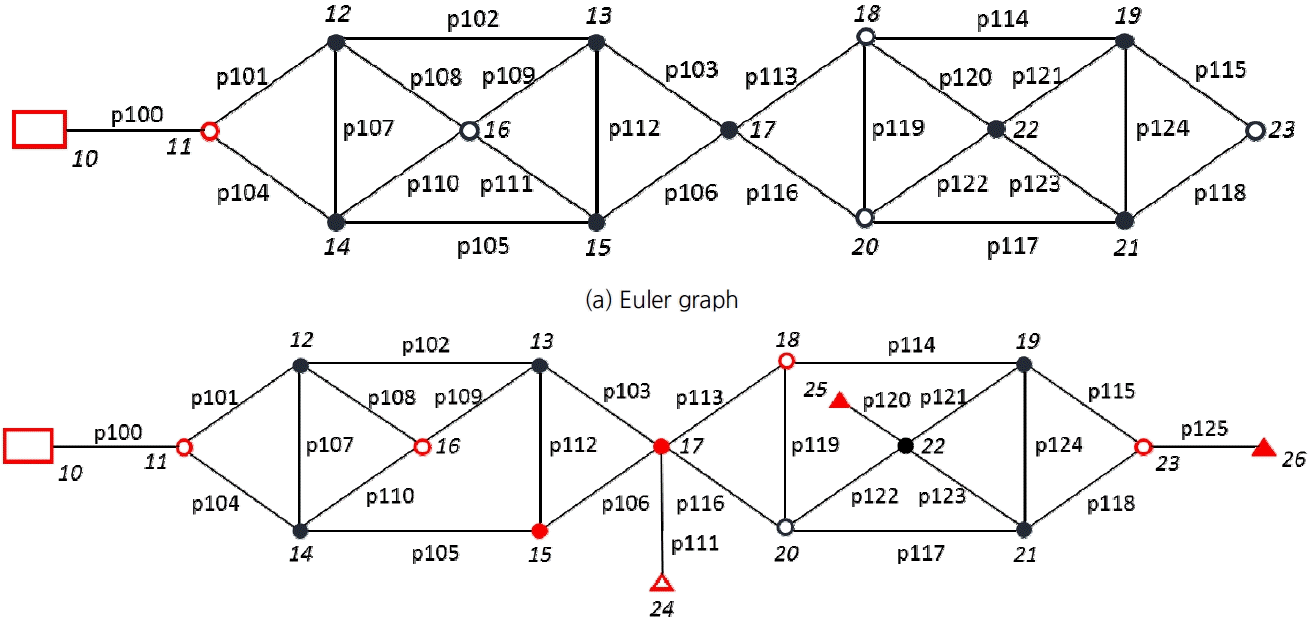
이에 Fig. 6에 나타낸 예시 관망 중 (a)는 홀수 차수 꼭짓점이 2인 Euler 그래프로 구성된 관망과 (b) non-Euler 그래프로 구성된 상수관망을 서로 비교하기로 하였다. Euler 그래프 상수관망은(Fig. 6(a)) 저수지(10)로부터 용수가 공급되는 관망을 구성하였으며, 홀수 차수 꼭짓점은 두 개의 연결 절점 10, 11에 해당하고 열린 경로를 가지고 있다. (a) 관망은 총관로수 25개, 홀수 절점수(저수지 제외) 1개, 짝수 절점수 13개, 총관로 길이 30,000 m로 구성되어 있다. (b) non-Euler 상수관망은 홀수 차수 연결절점이 10개로 구성되어 있으며 그림에서 빨간색으로 표시하였다. 본 관망은 총관로수 26개, 홀수 절점수(저수지 제외) 9개, 짝수 절점수 8개, 총관로 연장은 30,200 m로 구성되어 있다. 그림에서 식별의 편의를 위하여 저수지는 사각형(□), 연결관로가 1개인 절점은 삼각형(△), 기타 절점은 원(○)으로 표시하였다.
3.2. EPA-NET 모의
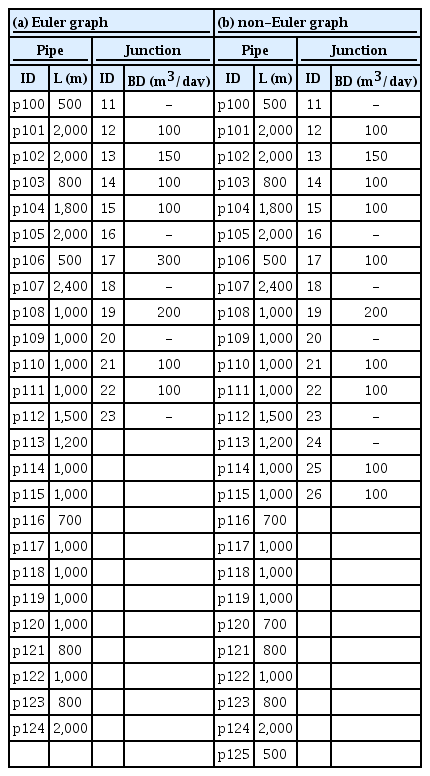
본 연구에서는 연구 대상인 Fig. 6의 두 개 가상 관망에 대하여 미국 환경청에서 배포하고 있는 EPANET2를 이용하여 관망 해석을 수행하였다. 관로 내의 물리적 특성인 관경, 길이, 조도계수 및 수요량 등을 이용하여 관로 내 각 지점과 시간별로 수리학적 특성인 관내에서의 유속과 절점에서의 압력분포를 예측할 수 있으며, 수질적으로 잔류염소 농도를 예측할 수 있다[12]. 연구 대상 관로의 관경(D, mm) 및 관로 연장(L, m)은 Table 1에 나타내었으며, 두 개의 가상 관망에 적용되는 관경은 100 mm를, 조도특성을 나타내는 C 값(Hazen-Williams 계수, 무차원)은 100을 모든 관로에 동일하게 적용하였다. 관로 연장 또한 p116을 제외한 모든 관로에서 Euler graph와 non-Euler graph의 값이 일치하며, non-Euler graph에서 추가된 p125관로의 연장은 500 mm를 할당하였다. EPANET2에서 고정수두 절점에 해당되는 저수지의 동수두는 100 m로 두 개의 관망에 동일하게 설정하였으며, 용수수요 절점의 표고(EL, m)는 절점 (18)에서 18.0 m로 설정한 것으로 제외하고 모든 절점의 표고를 ‘0’으로 설정하였다. 절점 (18)의 표고 만을 다른 절점들의 표고와 다르게 설정한 것은 최소 압력수두에 대한 비교를 원활하게 수행하기 위함이다. 기저 수요량(BD; Base Demand, m3/day)은 Table 1과 같이 절점에 할당하였다. Euler graph에서는 절점 (17)에 300 m3/day를 할당한 반면, non-Euler graph에서는 절점 (17), (25), (26)에 각각 100 m3/day를 할당하였다. Fig. 6에서 삼각형 또는 원의 내부가 채워져 있는 경우는 기저 수용량이 할당된 용수수요 절점을 나타내며, 비워져 있는 경우는 기저수요량이 없는 절점을 나타낸다. 이상의 EPANET2 입력자료를 이용하여 관망 해석한 결과는 절점에서의 압력과 잔류염소 분포를 도출하고자 하였다.
4. 결과 및 토의
4.1. Euler 그래프 관망 대상 모의 결과
EPANET2를 이용하여 Fig. 7(a) Euler 그래프 입력 관망을 대상으로 관망해석 결과를 나타낸 것이다. 절점에 표시된 수치는 압력수두(m), 관로에 표시된 수치는 유량(m3/day)을 나타낸다. 그 결과 최소압력수두는 16.90 m가 도출되었다. 본 예시 관망의 경우 이미 Euler 경로가 형성되어 있으므로 홀수 절점 연결관로 제거를 수행하더라도 그래프의 변화는 발생하지 않는다. 따라서 non-Euler 경로구성 방법인 3교차점 연결관로 제거를 수행하여 많은 조합을 도출하였는데 그 중 1개의 배치를 출력 관로(Fig. 7(b)로 나타낸 것이다. Fig. 7(b) 출력 관로는 총관로수 21개, 홀수절점수(저수지 제외) 5개, 짝수절점수 9개, 총관로길이 26,000 m, 최소압력수두 13.88 m로 나타났다. 입력 관로와 출력 관로 배치에 대한 비교에서 알수 있듯이, 총 4개의 관로를 제거하였으며, 관로의 길이는 4,000 m가 제거될 수 있음을 확인하였다. 반면 수리학적 관점에서 관로의 제거로 인한 최소압력수두 감소량은 3.02 m로써 상수관망을 운영하는데 문제를 발생시키지 않음을 예상할 수 있다.
4.2. non-Euler 그래프 관망 대상 모의 결과
Non-Euler 그래프 관망을 대상으로 홀수 절점 연결관로 및 3교차 연결관로 제거를 실행하는 경우 상수관망의 관로 및 절점 수가 많으며 제거 대상이 되는 관로의 수도 기하급수적으로 증가할 수 있다. 즉, 불필요한 관로로 제거 대상이 되는 관로의 수가 ‘n’이면 조합의 수는 ‘2n’만큼 증가하며, 전체 조합을 모의하는 데 많은 노력이 필요하다.
Fig. 8(a)는 앞서 언급한 non-Euler 그래프 입력 관망을 대상으로 EPANET2를 이용하여 수행한 관망해석 결과를 나타낸 것이다. 절점에 표시된 수치는 압력수두(m), 관로에 표시된 수치는 유량(m3/day)을 나타낸다. 본 관망은 총관로수 26개, 홀수절점수(저수지제외) 9개, 짝수절점수 8개, 총관로길이 30,200 m, 최소압력수두 11.92 m로 구성되어 있다.
Fig. 8(b)는 (a) 입력 관망을 대상으로 홀수 절점 연결관로 제거를 수행하여 많은 조합을 도출한 것 중 1개의 배치를 출력 관로로 예시한 것이다. (b)의 출력 관로는 총관로수 25개, 홀수절점수(저수지제외) 7개, 짝수절점수 10개, 총관로길이 29,000 m, 최소압력수두 3.41 m로 나타났다. Fig. 8(a)와 (b) 배치에 대한 비교에서 홀수 절점 연결관로를 제거하는 경우 총 1개의 관로를 제거하였으며, 관로길이는 1,200 m가 감소되었음을 확인하였다. 또한 수리학적 관점에서 관로 제거로 인한 최소압력수두 감소량은 8.51 m로 확인되었다.
또한 본 연구에서는 non-Euler 그래프 상수관망에 대하여 앞서 언급한 3교차점 연결관로 제거 개념을 적용하여 다양한 조합을 도출하였으며, 그 중 1개의 배치를 선정하여 Fig. 8(c) 출력 관로로 나타내었다. 이 출력 관로는 총관로수 21개, 홀수절 점수(저수지제외) 11개, 짝수절점수 6개, 총관로길이 25,200 m, 최소압력수두 0.40 m로 나타났다. 입력 관로와 출력 관로의 배치에 대한 비교에서 알 수 있듯이, 3교차점 연결관로 제거 개념으로 구성된 출력 관로의 경우 총 5개의 관로가 제거되었으며, 관로의 길이는 5,000 m 감소하였다. 또한 수리학적인 관점에서 관로 제거로 인한 최소압력수두 감소량은 11.52 m로 확인되었다.
본 연구에서 가상의 예시 Euler 및 non-Euler 그래프 상수관망을 대상으로 절점을 제거하고 새로운 관망을 구성한 결과 3교차점 연결관로 제거 개념이 보다 많은 관로를 제거함으로써 효율을 높일 수 있을 것으로 확인되었으나, 홀수 절점 연결관로 제거 개념은 상수 관망을 Euler 그래프로 형성함으로써 보다 합리적인 상수관망 설계 및 운영기법을 제시하는 것으로 판단된다.
5. 결 론
본 연구에서는 블록시스템의 단점인 과다한 절점 및 관로의 복잡성으로 인해 발생하는 손실 수두와 잔류 염소의 급격한 감소 문제를 해결할 수 있는 방안으로 제시된 ‘Eulerian path’개념과 Euerian path 개념과 상관없이 불필요한 관로를 제거할 수 있는 ‘non-Euler path’ 개념의 적용 타당성을 본 논문에서 제시하고자 하였다. 이에 다음과 같은 결론을 도출할 수 있었다.
1) 본 연구에서는 관망 전체를 완벽한 Eulerian path 개념을 적용하는 방법과 부분적으로 Non-Eulerian path 개념을 적용하는 ‘홀수 절점 제거’, ‘3교차점 연결관로 제거’, ‘수요량 없는 절점 제거’ 개념을 제시하고자 하였다. 상수관망에 완벽한 Eulerian path 개념을 적용할 수 없는 이유는 관망 내에 반드시 필요한 소화전 및 비상 용수 공급의 신뢰도(reliability)를 감할 수 없는 수요 절점 등이 존재하기 때문이다.
2) 본 연구에서 가상의 예시 Euler 및 non-Euler 그래프 상수관망을 대상으로 절점을 제거하고 새로운 관망을 구성한 결과 3교차점 연결관로 제거 개념이 보다 많은 관로를 제거함으로써 효율을 높일 수 있을 것으로 확인되었으나, 홀수 절점 연결관로 제거 개념은 상수 관망을 Euler 그래프로 형성함으로써 보다 합리적인 상수관망 설계 및 운영기법을 제시하는 것으로 판단된다.
3) 본 연구에서 제시하는 블록형 상수관망의 단점인 절점 및 관로의 복잡성으로 야기되는 문제를 해결하는 개념들은 아직 최적화 과정을 거치지 않았으며, 실제 운영 중인 관망을 대상으로 현장 검증을 완료하지 못한 측면에서 추후 보완 연구를 수행할 필요가 있다.
Acknowledgements
이 성과는 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구(No. 022R1A2C10064941161382116530101) 및 2020년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임(No. 2020R1I1A1A01070718).
Notes
Declaration of Competing Interest
The authors declare that they have no known competing interests or personal relationships that could have appeared to influence the work reported in this paper.