|
The Korean text of this paper can be translated into multiple languages on the website of http://jksee.or.kr through Google Translator.
AbstractObjectivesThis study was conducted to propose a new methodology for efficiently identifying and removing various outliers that occur in data collected through automated water quality monitoring systems. In the present study, water temperature data were collected from domestic G_water supply system, and the performance of the proposed methodology was tested for water temperature data collected from domestic G_water supply system.
MethodsWe applied the following analytical procedure to identify outliers in the water quality data: First, a normality test was performed on the collected data. If normality condition was satisfied, the Z-score was used. However, if the normality condition was not satisfied, outliers were identified using the quartile, and the limitations of the existing methodology were analyzed. Second, we decomposed the intrinsic mode function using empirical mode decomposition and ensemble empirical mode decomposition for the collected data, and then considered the occurrence of modal mixing. Finally, a group of intrinsic mode functions was selected using statistical characteristics to identify outliers. In addition, the performance of the method was verified after removing and interpolating outliers using regression analysis and Cook’s distance.
Results and DiscussionIn the case of water temperature data, as normality condition was not satisfied, outlier identification was carried out by applying the modified quartile method. It was confirmed that outliers distributed within the seasonal component could not be identified at all. In the case of empirical mode decomposition, modal mixing occurred because of the effect of outliers. However, in the case of the ensemble empirical mode decomposition, modal mixing was resolved and the distinct seasonal components were decomposed as intrinsic mode functions. The intrinsic mode functions were synthesized, which showed statistical correlation with the raw water temperature data. As a result of developing a regression model using the synthesized intrinsic mode functions and raw water temperature data and performing outlier search based on Cook’s distances, we concluded that various outliers distributed within the seasonal component could be effectively identified.
ConclusionsConsidering that satisfactory results could be derived from statistical analysis of the data collected from the automated water quality monitoring system, it can be concluded that outlier identification procedures are essential. However, in the case of the conventional univariate outlier search method, it is apparent that the outlier search performance is significantly poor for data with strong inherent variability, and the interpolation method for the searched outlier cannot be performed. Conversely, the outlier identification method based on ensemble empirical mode decomposition and regression analysis proposed in this study shows excellent discrimination performance for outliers distributed in data with strong inherent variability. Moreover, this method has the advantage of reducing the analyst’s dependence on subjective judgment by presenting statistical cutoff criteria. An additional advantage of the method is that data can be interpolated after removing outliers using intrinsic mode functions. Therefore, the outlier search and interpolation method proposed in this study is expected to have greater applicability as a more effective analysis tool compared to the existing univariate outlier search method.
요약목적본 연구는 국내 상수도 자동수질측정망을 통해 수집되는 자료에서 발생 가능한 다양한 이상치들을 효율적으로 탐색 및 제거 위한 방법론을 제안하기 위해 수행되었다. 이를 위해 국내 G_정수장으로부터 수온자료를 수집하였으며, 수집된 자료를 대상으로 이상치 방법론에 따른 적용 효과를 검정하였다.
방법본 연구에서 수질자료의 이상치 탐색을 위해 적용한 분석 절차는 다음과 같다. 첫째, 수집된 수온자료에 대해 정규성 검정을 수행하고 정규성을 만족하는 경우 Z-score, 정규성을 만족하지 않는 경우 사분위수를 활용하여 이상치를 탐색하고 기존 방법론의 한계점에 대해 분석한다. 둘째, 수온자료에 대해 경험적 모드 분해 및 앙상블 경험적 모드 분해를 활용하여 고유진동함수들을 분해한 후 모드 믹싱에 발생에 대해 고찰한다. 최종적으로 고유진동함수들의 통계적 특성치를 활용해 이상치를 식별할 기준 고유진동함수 집단을 선별한 후 회귀분석과 Cook 통계량의 절사 기준을 활용해 이상치를 제거 및 보간 후 그 성능을 검증한다.
결과 및 토의수온자료의 경우 정규성을 만족하지 못하며, 수정 사분위 방법을 적용하여 이상치 탐색을 수행한 결과 계절 성분 내에 분포하는 이상치들은 전혀 식별할 수 없다는 결과를 확인하였다. 경험적 모드 분해의 경우 이상치들의 효과로 인해 모드 믹싱 현상이 발생하였으나, 앙상블 경험적 모드 분해에서는 모드 믹싱이 해결되어 뚜렷한 계절 성분이 고유진동함수로서 분해되는 것으로 나타났다. 그리고 앙상블 모드 분해로부터 구해진 고유진동함수 중 원시 수온자료와 통계적 관계성이 높은 신호들을 합성하였다. 합성된 고유진동함수와 원시 수온자료를 활용해 회귀 모형을 개발하고, Cook 통계량 근간으로 이상치 탐색을 수행한 결과 계절 성분 내에 분포하는 다양한 이상치들을 효과적으로 탐색할 수 있는 것으로 분석되었다.
결론상수도 자동수질측정망을 통해 수집되는 자료들로부터 합리적인 통계분석 결과를 도출하기 위한 과정에서 이상치 탐색 작업은 필수적이라고 할 수 있다. 하지만 기존의 단변량 이상치 탐색 기법의 경우 고유 변동성이 강하게 분포하는 자료에 대해 이상치 탐색 성능이 현저히 떨어지며, 탐색된 이상치에 대한 내삽 방안도 제시하지 못한다는 한계가 명확하다. 반면, 본 연구에서 제시한 앙상블 경험적 모드 분해 및 회귀분석 기반의 이상치 탐색 방법은 고유 변동성이 강한 자료 내에 분포하는 이상치들에 대한 식별 성능이 뛰어나며, 통계적 절사 기준을 제시함에 따라 분석자의 주관적 판단을 최소화 할 수 있는 장점이 있다. 또한 앙상블 경험적 모드 분해 분석으로부터 구해진 고유진동함수들을 이용해 이상치 제거 후 자료 보간이 가능하다는 장점이 있다. 따라서 기존의 단변량 이상치 탐색 기법의 적용성에 대한 한계를 고려할 때 본 연구에서 제시한 이상치 탐색 및 보간 방안은 보다 효과적인 분석 도구로서 적용 가능할 것으로 기대된다.
1. 서 론상수도는 생활・공공・생산 활동에 필요한 양질을 물을 적절한 수압으로 연속적으로 공급하는 공공시설로 정의된다. 따라서 수원의 취수에서부터 도・송수, 정수, 배・급수 과정 전반에서 엄격한 수질관리는 상수도 운영의 핵심적인 기술적 요소이다. 국내 상수도 수질기준은 1963년 ‘건강진단 및 위생상에 관한 규정’ 제정을 통해 마련되었으며, 현재는 ‘먹는물 수질 기준(환경부, 2017)’에 의해 86개 항목에(수질기준 60종, 수질감시항목 26종) 대한 관리기준 및 처리방안이 수립되어 있다. 그리고 최근에는 환경정책기본법 등에 의거 국내 상수원 수질 보호와 수질오염사고 감시를 위해 전국의 주요하천 및 호소에 국가수질자동측정망을 설치함으로서 실시간 수질오염 감시와 대응을 위한 종합 물환경 감시체계를 운영 중에 있다[1,2].
수질자동측정망은 TMS (Tele-Monitoring system)로 연결됨에 따라 실시간의 연속적인 측정과 감시가 가능한 장점이 있으나 수동 수질측정에 비해 신뢰성이 떨어지는 단점이 있다. 즉, 자동측정 장비의 고장, 보정 및 통신설비 오류 그리고 관로상의 수리적인 요인 등으로 인해 측정 자료 내에 다양한 이상치(Outlier)들이 분포할 가능성이 높다. 수질자동측정 과정에서 발생되는 이상치들의 분포는 불가피하게 발생할 수밖에 없으나, 운영자가 원시자료를 그대로 분석에 사용할 경우 잘못된 결과가 도출된다. 이러한 분석오류를 방지하기 위해서는 측정 및 통신장비의 개선과 같은 구조적 대책과 더불어 원시자료 내에 분포하는 이상치를 탐색하기 위한 전처리 기법과 같은 비구조적 대책의 도입이 요구된다[3,4].
이상치 탐색 방법은 관측 자료의 차원에 따라 일변량(Univariate), 이변량(Bivariate), 다변량(Multivariate)로 분류된다. 그리고 통계적 분류에 따라 자료의 확률분포 또는 모수 추정을 기반으로 하는 모수적 방법(Parametric method)과 확률분포와 추정모수에 기반하지 않는 비모수적 방법(Non-parametric method)로 구분된다[5]. 일반적으로 상수도 시스템에서 관측되는 수질인자들의 경우 확률분포 그리고 상관관계에 대한 명확한 정보가 알려져 있지 않는 경우가 대부분이다. 따라서 수질인자들에 대한 이상치 탐색을 위해서는 각 수질인자들을 독립적인 관측값으로 인식하여 단변량 기반의 이상치 탐색 기법을 주로 적용하게 된다. 수질자료에 적용 가능한 단변량 이상치 탐색기법으로는 표준화 점수(Z-score), Dixon Q-test, Grubbs T-test, Rosner’s test 및 Walsh’s test 등이 있다. 하지만 상기의 방법론들은 정규분포에 대한 가정조건 및 상・하단에 위치한 일부 극값들에 대한 탐색만을 수행하게 되는 단점이 있다. 따라서 추세나 계절성분과 같이 자료의 고유 변동성(Inherent variability)이 강하게 분포하는 경우 변동 내부에서 분포하는 이상치들에 대한 탐색은 불가능하게 된다.
따라서 최근에는 기존의 단변량 이상치 탐색에 대한 대안으로서 관측된 자료에 내재된 주파수 성분의 형태 및 크기를 분석하는 분광분석이(Spectral analysis) 적용되고 있다. 분광분석의 대표적 방법론으로서 푸리에 변환(Fourier transform)과 웨이블릿 변환(Wavelet transform)이 있으나 비정상 시계열이나 비선형 변동을 나타내는 시계열을 다루는데 한계가 있으며, 특히 웨이블릿 변환의 경우 기저(Basis)의 선택에 따라 분석 결과가 상이하다는 문제가 존재한다[6]. 반면, Hung et al. [7]이 제시한 경험적 모드 분해(Empirical Mode Decomposition, EMD)는 비선형 비정상성 시계열 자료를 유한개의 고유진동함수(Intrinsic mode function)로 분해 해석함에 따라 시계열 분해에 대한 강건성을 가진다는 장점이 있다.
EMD를 활용한 이상치 탐색 연구로서 Lee & Ouarada [8]는 EMD의 출력정보를 활용해 이상기후 탐지 방안에 관한 연구를 수행하였으며, Loutridis [9], Park et al. [10]은 기계장치 분야의 이상신호 탐색을 위해 EMD를 적용하였다. 하지만 EMD는 원시자료 내에 임팩트 신호와 같이 연속적이지 않는 신호가 분포하게 되면 적정 고유진동함수로 분리되지 않고 여러 고유진동함수 내에 혼재되는 모드 믹싱(Modal Mixing)현상이 발생한다는 단점이 있다. 이러한 기존 EMD의 단점을 보완하기 위한 방안으로서 가우시안 노이즈를 원시자료에 합성하여 EMD를 반복 수행하는 앙상블 경험적 모드 분해법(Ensemble Empirical Mode Decomposition, EEMD)이 제안되었으며[11], Yang et al. [12], Sun et al. [13]은 수원에서 수집된 수질자료의 이상치 탐색 방안으로서 적용한 바 있다.
본 연구의 목적은 국내 상수도 시스템에서 자동측정망을 통해 관측・수집되는 수질자료 내에 분포하는 이상치를 탐색하고 제거하기 위한 전처리 기법의 제안에 있다. 선행연구들에서 살펴본 것과 같이 EMD 및 EEMD를 활용한 이상치 탐색은 원시자료를 다양한 주파수 대역의 고유진동함수로 분해함에 따라 추세 및 계절변동과 같은 고유변동이 강하게 분포하는 자료 내의 이상치 탐색에 대한 효율성이 높다는 장점이 있다. 따라서 본 연구에서는 국내 G_정수장으로부터 수집된 수질자료를 대상으로 기존의 단변량 이상치 탐색과 비교하여 EMD 및 EEMD 적용에 따른 이상치 탐색 효과를 검증하고, 이를 바탕으로 통계적 절사기준에 따른 수질자료 이상치 제거 방안을 제시하기 위한 연구를 수행하였다.
2. 이론적 배경EMD는 비선형 비정상 시계열 자료를 유한개의 고유진동함수로 분해하는 기법이다. 여기서, 고유진동함수는 신호의 극값의 수와 부호 변환점의 수가 같거나 하나의 차이만 존재하는 것 그리고 함수의 극댓값으로 이루어진 포락선과 극솟값으로 이루어진 평균값이 항상 0이어야 한다는 두 조건을 만족해야 한다. 원시시계열을 x(t)라 할 때 모든 극댓값 및 극솟값을 연결하는 상위 포락선(Upper envelope) u1(t)와 하위 포락선(Lower envelope) l1(t)을 구하고 두 포락선에 대한 평균값 m1(t)를 식 (1)과 같이 구한다.
식 (2)에서 구해진 h1(t)가 고유진동함수의 두 조건을 만족하는 경우 첫 번째 고유진동함수가 c1(t)되며, 그렇지 않은 경우 h1(t)가 고유진동함수의 조건을 만족할 때까지 시프팅(Shifting)과정을 식 (3)과 같이 j회 반복하게 된다.
상기의 과정을 통해 첫 번째 고유진동함수 c1(t)가 결정되면 원시시계열 x(t)에서 빼준 후 첫 번째 residue r1(t)를 식(4)와 같이 구하게 된다.
식 (4)로부터 구해진 r1(t)에 대해서 다시 상기의 과정을 반복해 ri(t)가 2개 미만의 극점을 가지게 될 때까지 반복하며, 최종적으로 n개의 고유진동함수 cn(t)를 구하게 되면 원시시계열 x(t)는 식 (5)와 같으며, 구하고자 하는 EMD의 결과가 된다.
하지만 앞 절에서 언급한 것과 같이 단순히 EMD기법을 신호분리에 적용하는 경우 각 고유진동함수의 신호 성분이 서로 섞여서 나타나는 모드 믹싱 현상이 발생되게 된다. 따라서 Wu and Huang [11]은 식 (6)에서 나타낸 것과 같이 원시 시계열 x(t)에 전 주파수 대역을 포함하는 화이트 노이즈 w(t)를 추가하는 EEMD 기법을 제안하였다.
3. 연구방법본 연구에서는 국내 상수도 자동관측시스템에서 수집된 수질자료에 대한 이상치 탐색 기법을 제안하기 위해 기존의 단변량 이상치 탐색 그리고 EMD, EEMD를 활용한 이상치 탐색 방법을 상호 비교하였다. 각 기법에 따른 이상치 탐색 성능을 분석하기 위해 국내 G_정수장으로부터 시단위의 수온 자료를 수집하였으며, 수집된 자료의 기술통계량은 Table 1에 정리하였다.
그리고 Chen and Liu [14]는 시계열 자료에서 발생될 수 있는 이상치들의 분포를 다음의 4가지 형태로 분류하였다.
1) 가법적 이상치(Addictive outlier, AO): 시간 t=t0에서 시계열 자료 중 하나가 지나치게 크거나 작은 값을 갖는 경우
2) 혁신적 이상치(Innovational outlier, IO): 시간 t=t0 이후 시계열의 보행이 기존의 보행과는 달리 전혀 다른 분포를 나태는 경우
3) 수준이동 이상치(Level shift outlier, LSO): 시간 t=t0 이후에 시계열 전체가 상하로 이동하는 경우
4) 일시적 변화 이상치(Temporary chance outlier, TC): 시간 t=t0에서 일시적으로 시계열이 이동하였으나 지수적으로 신속히 원래의 분포로 수렴하는 경우
본 연구에서는 수질 시계열 자료에서 발생 가능한 주요 4가지 형태의 이상치들을 효과적으로 탐색하기 위한 연구를 수행하였으며, 분석 절차는 다음과 같다. 첫째, 수집된 수온자료에 대해 정규성 검정을 수행하고 정규성을 만족하는 경우 Z-score, 정규성을 만족하지 않는 경우 사분위수(Quartile)를 활용하여 이상치를 탐색하고 기존 방법의 한계점에 대해 분석한다. 둘째, 수온자료에 대해 EMD 및 EEMD를 활용하여 유한개의 고유진동함수를 산정한 후 모드믹싱에 발생에 대해 고찰한다. 최종적으로 선택된 고유진동함수들의 평균주기, 상관계수와 같은 특성치를 활용해 잠재적 이상치 후보를 분리할 고유진동함수 집단을 선별한 후 통계적인 절사기준에 따라 이상치를 제거하여 그 성능을 검증한다. 그리고 본 연구에서는 EMD 및 EEMD 구현을 위해 MathWorks사에서 개발한 Matlab 2019b를 활용하였다.
4. 연구결과
Fig. 1은 국내 G_정수장에서 수집된 수온자료의 시계열 분포 및 정규성 검정 결과를 도시한 것이다. Fig. 1(a)에서 나타낸 것과 같이 원시 수온자료에는 계절변동이 강하게 분포하며, 자료전반에 걸쳐 AO형태의 이상치 후보군들이 분포하는 것을 알 수 있다. 그리고 2013년 7월, 2014년 9월에 수온변화가 크게 발생되는 수준이동(Level shift)이 발생되었으며, IO, LSO 및 TC형태의 이상치 후보군들도 자료 전반에서 분포하고 있다. 그리고 수온자료의 히스토그램(Fig. 1(b))을 살펴보면 자료의 상・하단에서 빈도가 높게 나타나는 비대칭 분포를 나타내며, Q-Q plot (Fig. 1(c))에서도 양 끝에서 직선을 많이 벗어나므로 정규분포를 따르지 않는 것으로 판단된다. 따라서 비정규성을 나타내는 수온자료의 이상치 탐색을 위해 왜도(Skewness)에 대한 로버스트(Robust) 통계량인 Medcouple (MC)을 활용한 수정 사분위수(Adjusted quartile) 방법을 적용하였으며, MC에 따른 이상치 탐색 조건은 다음과 같다[15].
여기서, mn는 개수가 n인 자료의 중앙값, 핵함수(Kernel function) h(∙,∙)는 모든 xi ≠ xj에 대하여 식 (9)와 같이 정의 된다.
그리고 제1사분위수(Q1), 제3사분위수(Q3) 및 MC에 따른 이상치 탐색 조건은 식 (10)과 같다.
여기서, IQR=Q3-Q1이다.
Table 2는 수온자료에 대해 수정 사분위수 방법을 적용하기 위해 산정된 각 매개변수 및 이상치 탐색 결과를 정리한 것이다.
각 매개변수로부터 산정된 수정 사분위수의 이상치 탐색 조건 및 결과를 살펴보면 상・하단 경계값은 (35.48℃, -30.10℃)이며 수온자료의 최대・최솟값은 (26.43℃, 0.43℃)임에 따라 이상치 탐색점 결과는 ‘0’이 된다. 즉, 수정 사분위수 방법의 경우 원시자료 내에 강한 계절성분이 분포하는 경우 계절성분의 변동 범위 내에서 발생되는 이상치들에 대해서는 전혀 탐색할 수 없다는 한계점을 명확하게 알 수 있다. 따라서 본 연구에서는 원시 수온자료 내에 분포하는 다양한 이상치들을 탐색하기 위해 EMD 및 EEMD를 적용하였으며, 그 결과는 Fig. 2와 Fig. 3에 나타내었다.
Fig. 2는 EMD를 이용하여 분해된 고유진동함수들의 결과를 나타낸 것으로 단기변동을 나타내는 고유진동함수 1~4에서 AO형태의 이상치 후보군들의 분포가 뚜렷하게 나타나는 것을 알 수 있다. 하지만 AO형태의 이상치 및 기타 이상치들의 효과로 인해 중・장기 변동을 나타내는 고유진동함수 5~8 그리고 계절변동을 나타내는 고유진동함수 9~10에서 주파수 성분이 혼재되는 모드믹싱 현상이 발생되는 것을 알 수 있다.
반면, Fig. 3은 앙상블 멤버 수 k=1,000, 화이트 노이즈 w(t)의 진폭을 수온자료 표준편차의 0.2배로 입력하여 수행한 EEMD 결과를 나타낸 것으로, AO형태를 포함한 이상치 후보군 대부분이 고유진동함수 1~6에서 분포함에 따라 고유진동함수 9에서 보다 뚜렷한 계절성분이 분리됨을 알 수 있다.
Sun et al. [13]은 EMD와 EEMD로부터 분해된 고유진동함수를 활용해 이상치 탐색을 수행하기 위한 방안으로 원시자료의 변동과 비교해 상대적으로 높은 적합도를 만족하는 고유진동함수들을 합성한 후 원시자료와의 상대오차(relative error)를 이상치 탐색의 절사기준으로 적용하는 방안을 제시하였다. 이에 본 연구에서는 EEMD로부터 분해된 각 고유진동함수들의 적합도 정도를 분석하기 위해 통계적 특성치를 산정하였으며, 그 결과는 Table 3에 요약하였다.
원시 수온자료로부터 분해된 고유진동함수들의 평균주기를 살펴보면 고유진동함수 1~3은 1일(24 hr) 이하의 단기변동, 고유진동함수 4~6은 2.2일(53 hr)~12.7일(305 hr) 범위의 중기변동, 고유진동함수 7~8은 36.1일(867 hr)~188.8일(4,530 hr) 범위의 장기변동, 고유진동함수 9은 388.6일의 계절변동으로 판단된다. 그리고 원시 수온자료와 각 고유진동함수들의 분산비율을 살펴보면 고유진동함수 1~8의 누적 분산비율은 4.0%인 반면 고유진동함수 9의 분산비율은 61.8%로서 전체변동에 대해 가장 높은 기여도를 나타내었다. 또한 원시 수온자료에 대한 각 고유진동함수들의 상관계수를 살펴보면 고유진동함수 1~7의 상관계수는 최대 0.08인 반면, 고유진동함수 8~9의 상관계수는 0.80 이상으로 강한 상관관계를 나타내었다.
이상치 탐색을 위해 고유진동함수의 합성 시 고려사항으로 고유진동함수의 평균주기, 전체분산에 대한 기여도 그리고 원시 자료에 대한 상관관계가 있다. 본 연구에서는 각 조건의 조합을 고려해 3가지의 case로 구분하여 고유진동함수를 합성하였으며, 그 결과는 Table 4에 요약하였다.
case I의 경우 전체분산에 대한 기여도만을 고려해 합성된 고유진동함수들이며 원시 수온자료에 대해 강한 상관관계(c.c.=0.987)를 만족하지만, Fig. 4(a)에서 도시한 것과 같이 상・하단 변곡점에서 높은 편차를 나타내었다. case II의 경우 분산 기여도, 상관관계를 고려해 합성한 고유진동함수이며 Fig. 4(b)에서 도시한 것과 같이 변곡점에서의 편차는 감소하기는 하나 지나친 평활화 효과로 인해 원시 수온자료의 수준이동이 발생한 2013년 7월, 2014년 9월 기간에서는 상대적으로 높은 편차를 나타내었다. 반면, case III는 분산 기여도, 상관관계 및 장기변동 이상의 주기를 모두 고려해 합성된 고유진동함수로서 Fig. 4(c)에서 도시한 것과 같이 전체 시계열 구간에서 원시 수온자료와의 높은 적합도를 나타내는 것을 알 수 있다. 따라서 본 연구에서는 case III에서 제시한 합성 고유진동함수를 이상치 탐색을 위한 기준 signal로 채택하였다.
EEMD로부터 합성된 고유진동함수를 이용해 원시 자료내의 이상치를 탐색하기 위해서는 객관적인 이상치 절사기준이 요구된다. 하지만 Sun et al. [13] 등의 선행연구에서는 단지 원시자료와 합성된 고유진동함수 사이의 상대오차(relative error)를 이상치 탐색의 절사기준으로 적용하는 등 객관적인 기준을 제시하지 못한 한계가 있다. 이에 본 연구에서는 원시자료와 합성된 고유진동함수를 활용하여 이상치를 탐색할 수 있는 통계적인 절사기준을 제시하기 위해 선형회귀분석을 활용하는 방안을 적용하였다.
선형회귀분석에 있어서 자료 내에 분포하는 이상치들은 회귀계수 추정에 큰 영향을 미치게 되며, 이러한 이상치들은 영향력 관측치(influential observation)로 정의된다. 영향력 관측치를 판단하기 위한 방법론으로 식 (11)과 같이 정의되는 Cook 통계량(Cook’s distance) [16]이 가장 널리 적용되고 있으며, Kim & Storer [17]가 제안한 영향력 관측치 절사기준은 식 (12)와 같다.
따라서 본 연구에는 원시 수온자료와 case III의 합성 고유진동함수를 이용해 선형회귀 모형을 개발하고 각 관측 값에 대한 Cook 통계량 및 식 (12)에서 제시한 절사기준을 활용해 이상치 탐색을 수행하였다. 그리고 Table 5는 설명변수로 원시 수온자료, 반응변수로 합성 고유진동함수를 입력해 개발된 선형회귀모형 및 Cook 통계량 산정 결과를 요약한 것이다.
그 결과 선형회귀모형의 R2=0.997으로 높은 설명력을 만족하였으며, 회귀계수 및 모형 적합도 검정 모두 유의수준 5%하에서 유의미한 것으로 분석되었다. 그리고 Cook의 통계량은 0.00~0.03의 범위에서 분포하였으며, 전체 자료의 크기 및 회귀모형의 형태에 따른 Cook의 통계량 절사기준은 0.00016으로 산정되었다.
최종적으로 Table 5에서 제시한 각 관측 값의 Cook 통계량 및 절사기준에 따라 수온자료에 대해 영향력 관측치 분석을 수행한 결과 647개(2.8%, 원시 수온자료: 22,608개)의 이상치들이 탐색되었으며, 그 결과는 Fig. 5에 나타내었다.
Fig. 5(a)는 원시 수온자료와 합성된 고유진동함수의 산포도 및 영향력 관측치 탐색결과를 함께 도시한 것으로, 산포도 곡선 하단에 위치한 대부분의 영향력 관측치들은 AO 형태의 이상치로 예상된다. Fig. 5(b)는 원시 수온자료의 시계열, Cook 통계량 및 절사기준을 활용해 식별된 이상치들의 분포를 함께 도시한 것으로, 수온자료의 수준이동에 따른 LSO 형태의 이상치 및 일시적인 형태의 IO 및 TC 형태의 이상치로 예상되는 집단 대부분이 식별되는 것을 알 수 있다. 그리고 Fig. 5(c)는 원시 수온자료에서 이상치를 제거한 후 발생된 결측값들에 대해 합성된 고유진동함수의 결과를 이용해 자료 보간(interpolation)을 수행한 결과를 나타낸 것으로, 원시자료 전반에서 분포하는 AO형태의 이상치 그리고 2013년 7월, 2014년 9월 기간에서 LSO형태의 이상치 대부분이 보간됨에 따라 원시 수온자료의 고유변동성이 더욱 명확하게 나타나는 것을 알 수 있다.
5. 결 론본 연구는 국내 상수도 자동수질측정망을 통해 수집되는 자료에서 발생 가능한 다양한 이상치들을 효율적으로 탐색 및 제거 위한 방법론을 제안하기 위해 수행되었다. 이를 위해 추세 및 계절변동과 같은 고유변동이 강하게 분포하는 자료의 이상치 탐색에 대해 효율성이 높은 것으로 평가되는 EEMD 기법을 적용하였으며, 선형회귀 분석을 활용한 통계기반의 이상치 절사기준을 제시하였다. 그리고 본 연구에서 제시한 주요 연구 결과들은 다음과 같다.
1) 본 연구에서는 국내 G_정수장 수질자료 중 계절 성분이 강하게 분포하는 수온자료를 대상으로 이상치 탐색을 수행하였다. 그리고 수온자료에 대한 정규성 검정 결과에 따라 수정 사분위 방법을 적용하여 이상치를 탐색을 수행한 결과 계절성분 내에 분포하는 이상치들에 대해 전혀 탐색할 수 없다는 결과를 확인하였다.
2) 기존의 단변량 이상치 탐색에 대한 대안으로서 분광분석 기법인 EMD 및 EEMD를 적용하였다. EMD의 경우 수온자료 전반에 분포하는 다양한 이상치의 분포로 인해 분해된 각 고유진동함수에 신호성분이 혼재되는 모드 믹싱이 발생되었으나, 일정 대역의 무작위 화이트 노이즈를 추가하여 수행된 EEMD는 대부분의 이상치들이 단기변동에 분포함에 따라 보다 효율적으로 장기 및 계절성분 분해가 가능한 것으로 분석되었다.
3) 이상치 탐색을 위한 기준 고유진동함수들의 합성을 위해 통계적 특성치들을 분석한 결과 전체분산에 대한 기여도, 상관관계 그리고 장기변동 이상의 주기를 모두 고려한 경우가 원시 수온자료와의 적합도 및 상대오차 정도가 가장 우수한 것으로 분석되었다.
4) 상기의 조건에 따라 합성된 고유진동함수 및 원시 수온자료를 대상으로 선형회귀모형을 개발한 후 Cook 통계량을 산정하고 Kim & Storer [17]가 제안한 절사기준을 근간으로 이상치 탐색을 수행한 결과 강한 계절변동 내부에서 임팩트 형태로 분포하는 AO 형태의 이상치 대부분이 탐색되었다. 또한 원시 수온자료의 수준이동에 따른 LSO 형태의 이상치, 지역적으로 발생되는 IO 및 TC 형태의 이상치 집단들도 효과적으로 탐색할 수 있는 것으로 분석되었다.
상수도 자동수질측정망을 통해 수집되는 자료들로부터 합리적인 통계분석 결과를 도출하기 위한 과정에서 이상치 탐색 작업은 필수적이라고 할 수 있다. 하지만 기존의 단변량 이상치 탐색 기법의 경우 고유변동성이 강하게 분포하는 자료에 대한 이상치 탐색 성능이 현저히 떨어지며, 탐색된 이상치에 대한 내삽 방안도 제시하지 못한다는 한계가 명확하다. 반면, 본 연구에서 제시한 EEMD 및 회귀분석 기반의 이상치 탐색방법은 고유변동성이 강한 자료 내에 분포하는 이상치들에 대한 식별성능이 뛰어나며, Cook 통계량 기반의 객관적 절사기준을 제시함에 따라 분석자의 주관적 판단을 최소화 할 수 있는 장점이 있다. 또한 EEMD부터 구해진 고유진동함수들의 합성을 통해 이상치 제거 후 자료 보간이 가능하다는 장점이 있다. 따라서 기존의 단변량 이상치 탐색 기법의 적용성에 대한 한계를 고려할 때 본 연구에서 제시한 EEMD 및 회귀분석 기반의 이상치 탐색 및 보간 방안은 보다 효과적인 분석 도구로서 적용 가능할 것으로 기대된다.
NotesDeclaration of Competing Interest The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper. Fig. 5.Outlier detection and interpolation results using linear regression model and Cook’s distance. 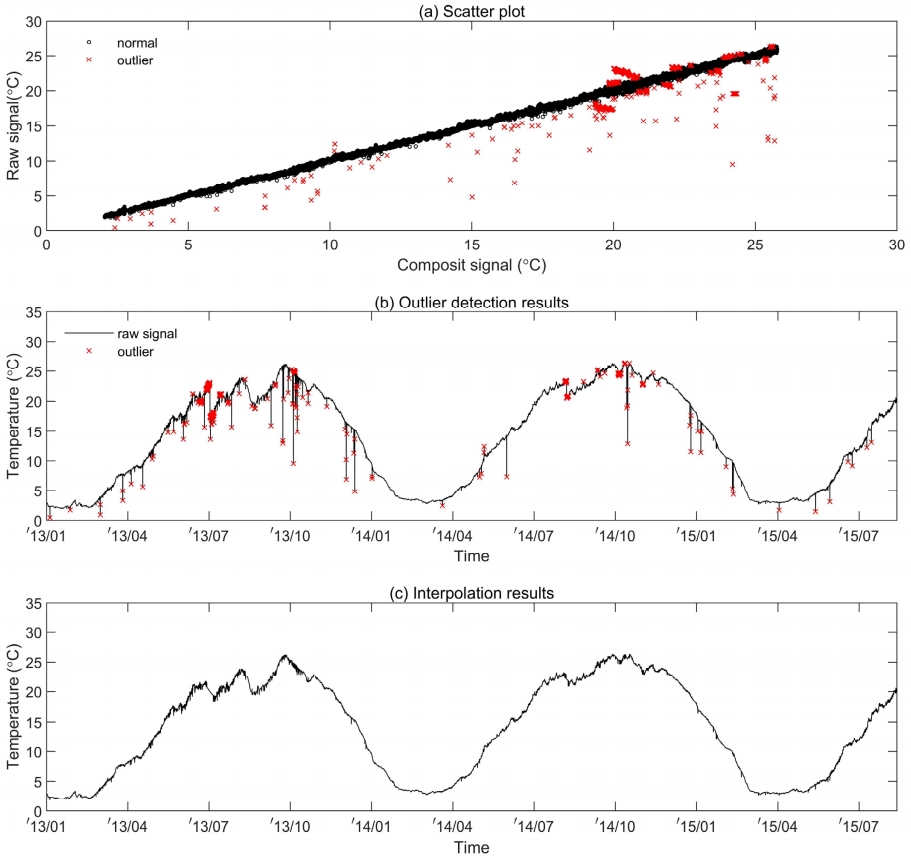
Table 1.Statistical characteristics of temperature (℃) data at G_WTP.
Table 2.Outlier detection result using adjusted quartile.
Table 3.Variance, correlation and mean period of signals. Table 4.Statistical test results for composite intrinsic mode functions. References2. Korea Ministry of Environment and Korea Environment Corporation Home Page, http://www.waternow.go.kr(2021)
3. J. Kim, N. Park, S. Yun, S. Chae, S. Yoon, Application of isolation forest technique for outlier detection in water quality data, J. Korean Soc. Environ. Eng., 40(12), 473-480(2018).
4. S. M. Yoon, S. S. Kim, S. H. Chae, N. S. Park, Introducing new outlier detection method using robust statistical distance in water quality data, Desalin. Water Treat., 149, 157-163(2019).
5. S. H. Lee, Outlier detection and treatment using R Free Academy, Paju, Korea(2015).
6. Y. J. Kim, J. C. Yoon, S. Y. Jei, A study for relative purchasing power parity using a empirical mode decomposition, JKDAS., 16(2), 785-793(2014).
7. N. E. Huang, Z. Shen, S. R. Long, M. C. Wu, H. H. Shih, Q. Zheng, N. C. Yen, C. C. Tung, H. H. Liu, The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis, in Proceedings of the Royal Society of London A Mathematical, Physical and Engineering Sciences, Proc. R. Soc. Lond. ALondon, pp. 903-995(1998).
8. T. Lee, T. B. M. J. Ouarda, Stochastic simulation of nonstationary oscillation hydroclimatic processes using empirical mode decomposition, Water Resour. Res., 48(2), W02514(2012).
9. S. J. Loutridis, Damage detection in gear systems using empirical mode decomposition, Eng. Struct., 26(12), 1833-1841(2004).
10. S. H. Park, J. H. Choi, A study on fault classification by eemd application of gear transmission error, J. Comput. Struct. Eng. Inst. Korea., 30(2), 169-177(2017).
11. Z. Wu, N. E. Huang, Ensemble empirical mode decomposition: a noise-assisted data analysis method, Adv. Adapt. Data Anal., 1(1), 1-41(2009).
12. Z. Yang, Y. Liu, D. Hou, T. Feng, Y. Wei, J. Zhang, P. Huang, G. Zhang, Water quality event detection based on multivariate empirical mode decomposition, in Proceedings of 2014 IEEE International Conference on Systems, Man, and Cybernetics, IEEE. San Diego, pp. 2663-2668(2014).
13. G. Sun, P. Jiang, H. Xu, S. Yu, D. Guo, G. Lin, H. Wu, Outlier detection and correction for monitoring data of water quality based on improved VMD and LSSVM, Complexity., 2019, 12(2019).
14. C. Chen, L. M. Liu, Joint estimation of model parameters and outlier effects in time series, J. Am. Stat. Assoc., 88(421), 284-297(1993).
15. M. Hubert, E. Vandervieren, An adjusted boxplot for skewed distributions, Computational Statistics&Data Analysis., 52(12), 5186-5201(2008).
16. R. D. Cook, Detection of influential observation in linear regression, Technometrics., 19(1), 15-18(1977).
17. C. R. Kim, B. E. Storer, Reference value for Cook’s distance, Commun. Stat.-Simul. Comput., 25(3), 691-708(1996).
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||