1. 서 론
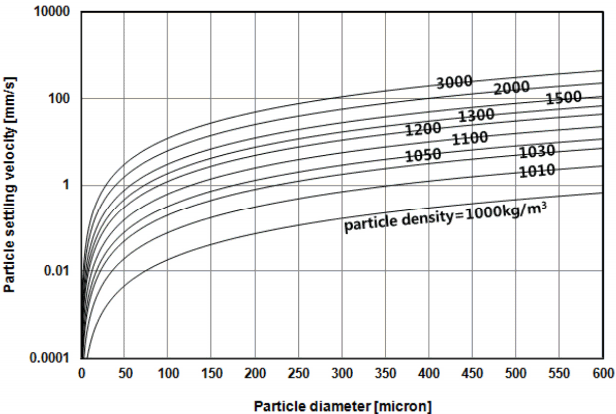
침전공정은 수처리 공정 중 중력의 힘을 이용하여 고체와 액체를 분리하는 공정중의 하나이다. 그러나 침전지의 수리적 구조, 유량변동, 유출부 등 세부인자로 이루어져 있어서 국부적인 에너지의 소산, 단락류 및 밀도류, 사수부의 발생 등 복잡한 흐름 특성으로 수처리 효율이 만족스럽지 못한 경우가 자주 발생하며[1,2] 세부인자의 형상에 의해 침전지내의 유동특성과과 침전효율이 크게 좌우 되는 것으로 알려져 있다[3]. 많은 연구자들이 침전지의 유동특성과 침전효율을 예측하기 위한 수치모형을 개발하였다[4~6]. Computational Fluid Dynamics (CFD, 전산유체역학)를 이용하여 다양한 조건에서 침전지내의 유동특성을 예측하였으며[7] 침전지에 관한 실험적 연구로는 Acoustic Doppler Velocimeter (ADV)를 이용하여 정방형 모형 침전지에 대해 유속과 난류 성분을 측정하였다[8]. Salem 등[9]은 경사판이 설치된 침전지내의 체류시간을 CFD로 해석하였으며, Park 등[10]은 CFD와 ADV를 이용하여 병렬 배열형 상향류식 침전지내로 유입되는 유량의 시간적인 편차로 인한 침전지 내 수리적 구조에 대하여 연구하였다. 그러나 이러한 연구들은 대부분 침전지의 수리구조 개선이나 속도분포에 초점을 두고 있다. 식 (1)은 Stokes가 제시한 입자의 침적 속도이며, Fig. 1은 식 (1)의 입자 크기, 밀도를 달리한 경우의 침전 속도를 나타내고 있다. 그러나 실제 현상에서는 입자가 침전하는 경우 주위의 유도흐름에 의하여 침전속도는 상이하게 나타난다. 침전지의 설계단계부터 침전내의 유동특성 뿐만 아니라 플럭에 대한 침전효율의 data가 필요하며 이것을 근거로 침전지의 수리적 구조 설계에 반영되어야 한다.
여기서 Vs는 침전속도[m/s], g는 중력가속도[m/s], d는 입자의 직경[m], v는 동점성계수[m2/s], ρs는 입자의 밀도[kg/m3], ρw는 물의 밀도[kg/m3]이다.
이에 본 연구에서는 설치 운영 중인 D_정수장의 장방형 침전지를 대상으로 설계유량과 운영 유량에 대하여 침전지의 유동특성 및 tracer 모의를 수행하였으며, 침전지의 유입부로 유입되는 플럭을 입자로 가정하여 모사하는 Lagrangian기법을 적용하여 침전지의 효율을 검토하였다. 그리고 이론적 Stokes의 침전속도를 기본으로 한 침전지의 침전 효율을 비교 검토하였다.
2. 수치해석
2.1. 침전지 및 수치해석 대상
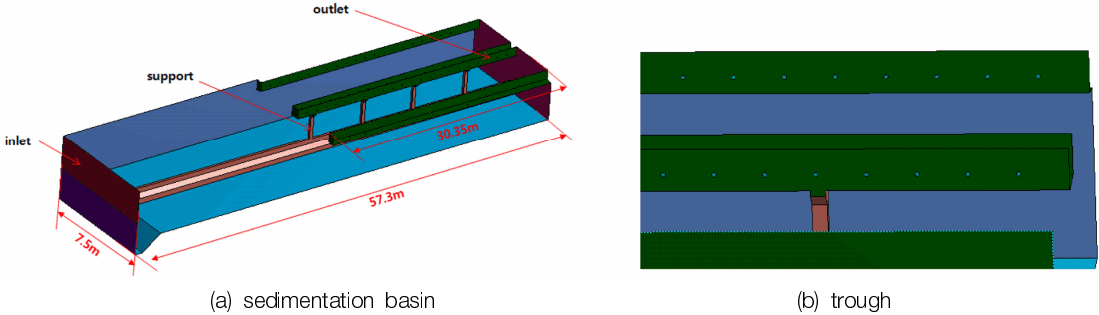
Fig. 2는 본 연구를 위하여 국내 D_정수장의 침전지의 개략도를 나타내고 있다. 침전지는 6지로 구성되어 있으며, 전단부의 응집지를 지나 침전지의 유출 트라프(trough)를 통해 유출된다. 해석 영역은 6지가 모두 같은 형상이므로 1지에 대하여 Fig. 2에 표시한 영역과 같이 응집지 출구부부터 침전지 트라프까지를 대상으로 하였다. Fig. 3(a)는 본 해석에 적용된 침전지 형상으로서 유로방향으로 57.3 m, 유로수직방향으로는 7.5 m의 크기를 갖는다. 그리고 높이 방향으로는 자유수면 높이에 해당하는 6.0 m이며, 침전지 바닥면은 경사도 0.3/51.7로 기울어져 있다. 유출 트라프의 길이는 30.35 m이며 유출 트라프의 각 측면과 바닥면에 오리피스 구조의 물의 유출공이 존재한다. 유출공의 직경은 30mm로서 트라프 측면 88개 총 4면에 353개의 유출공이 존재하며, 바닥면에는 14개의 유출공 총 3면에 42개의 유출공으로 이루어져 있다. 모든 유출공 전산모사 수행시 과도한 격자분포로 계산효율성이 저하됨으로 유출공의 직경 φ120mm로 가정하여 측면에 22개, 바닥면에 10개로 구성하였다. 정수장 침전지의 유량조건은 Table 1과 같이 설계유량(33,333m3/day)과 운영유량(15,864 m3/day)에 대하여 각각 해석이 수행되었으며, 설계 유량이 운영유량보다 약 2배 정도 높은 유량값을 갖는다.
2.2. 수치해석 방법
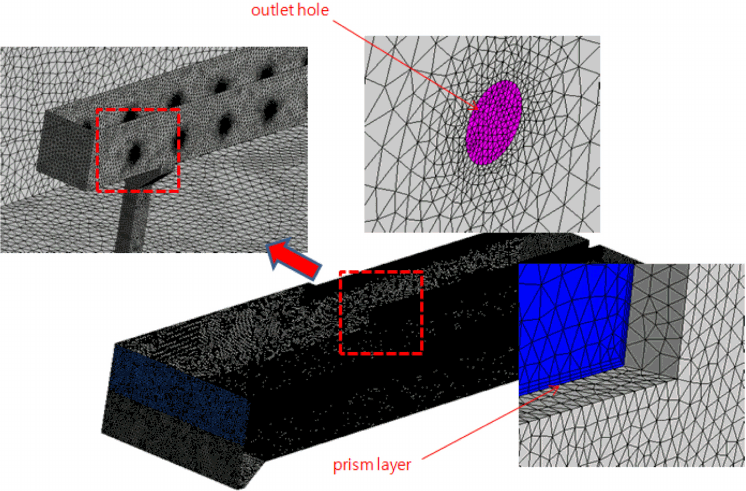
Fig. 4은 표면상의 계산 격자 분포를 나타내고 있으며, 격자 생성 툴인 ANSYS 소프트웨어를 사용하여 hybrid type의 격자를 생성하였다[11,12]. 그리고 벽면 근처와 작은 엣지(edge)에 대한 해상을 보다 정확하게 하기 위하여 조밀한 격자 분포를 적용하였다. 격자수는 2,680,000개 노드수(elements 12,032,000개)를 적용하여 수행하였다. 수치계산은 상용프로그램인 ANSYS CFX 12.1을 사용하였으며[11,12], 경계조건으로 입구에는 설계유량과 운영유량에 해당하는 질량유량조건, 출구에는 대기압 조건을 적용하였으며, 벽면 조건으로는 no-slip condition을 적용하였다. 그리고 자유수면에 해당하는 부분은 slip condition을 적용하였다. CFD 모사 시 난류모델의 선정이 정확도를 좌우할 수 있으며, 통상 수처리 공정에 적용되는 난류모델은 선행 연구자들이 적용한 standard k-e 난류모델을 사용하였다[13,14].
침전 효율을 구하가 위하여, 침전지 입구에서 균일한 입자분포를 주입시켜 출구영역으로 나오는 입자의 수를 측정하여 계산하였다. 물과 입자 간에는 물에 의하여 입자가 영향을 받아 입자의 거동을 결정하는 one-way coupling method를 적용하였으며, 물속의 입자가 받는 항력의 영향을 고려하기 위하여 다음의 식 (2)의 Shiller Nauman drag force를 적용하였다[11,12].
여기서 Re는 Reynolds number를 나타낸다.
2.3. 추적자 시험 모사 방법
일반적으로 체류시간 분포에 대한 정보는 유입수에 추적자(tracer)를 유입시키고 유출수에서 추적자의 농도를 측정하는 추적자 시험을 통해 얻을 수 있다. 추적자의 농도를 시간에 따른 곡선을 그려 그 형태를 무차원화하여 추적자 곡선을 상대적으로 비교하였다. Tracer의 유출 양상을 이용하여 조 내의 plug flow와 mixing의 정도, 그리고 단락류의 정도 등의 수리학적 효율을 분석하는 방법에는 여러 가지가 알려져 있으나, 대표적으로 Index법과 Rebhun & Argaman법이 주로 사용되어지고 있으며 본 연구에서는 Table 2에 정의된 Index법을 사용하여 평가하였다.
CFD 해석을 통한 추적자(Tracer) 해석은 계산영역의 입구에서 출구까지 유체(물)의 소요되는 시간을 측정하는 방법으로 additional variable로 수행한다. Additional variable은 수송방정식에서 계산되는 속도, 압력 등과 같이 하나의 변수로 처리하여 계산하는 방법이다. CFX 수치해석에서 additional variable에 대한 수송 방정식의 일반 형태는 식 (3)과 같이 왼쪽의 시간에 대한 항, 대류항 그리고 오른쪽에는 확산항, 소스항으로 구성된다.
난류 유동을 위한 Reynolds-averaged 방정식은 식 (4)와 같이 다시 표현된다.
여기서, U는 계산 도메인의 유체 속도, ρ는 단위 체적당 밀도, ϕ는 단위 체적 또는 농도당 보존된 양, φ=ϕ/ρ는 단위 질량당 보존된 양, Sφ는 단위 체적 단위 시간당 보존되는 양의 단위를 가지는 체적의 소스항, Dφ는 스칼라에 대한 운동학적 확산, Sct는 난류 Schmidt number, μt는 난류 점성을 나타낸다.
유동계산은 비정상상태 즉 시간 변화에 따른 유동을 계산하며, 추적자(tracer)라는 스칼라양으로 유체 거주 시간을 계산하기 위하여 변수로 설정하며, 단위는 [kg/m3]으로 설정한다. 경계조건으로 입구에서 단위 체적당 질량의 단위로 설정하고, 정상상태 계산을 초기조건으로 하여, 식 (5)와 같은 tracer 양으로 입구에서 유입된다고 가정한다.
여기서, step 함수는 괄호 안의 값이 음의 값이면 0, 양의 값이면 1을 반환하는 CFX에 제공하는 함수이며, t는 시간을 나타낸다.
CFX 프로그램을 활용한 추적자 실험 시 단지 입구에서 출구까지의 tracer 변수의 시간만 관심의 대상이므로 계산의 편의를 위하여 식 (5)에서 최대양을 1 [kg/m3]로 설정하였다. 또한, 후처리에서 시간 변화에 따른 출구영역의 무차원 농도 및 입구에서 주입된 전체 tracer 양에 대한 출구에서 유출된 전체 tracer의 양을 백분율로 표현하였다.
3. 결과 및 고찰
3.1. 침전지 유동특성
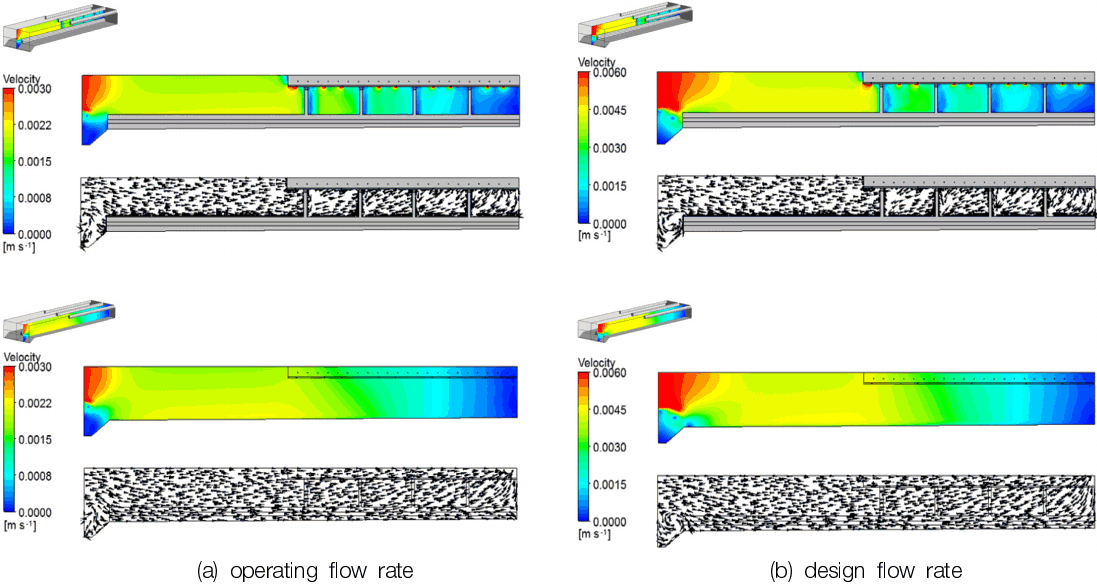
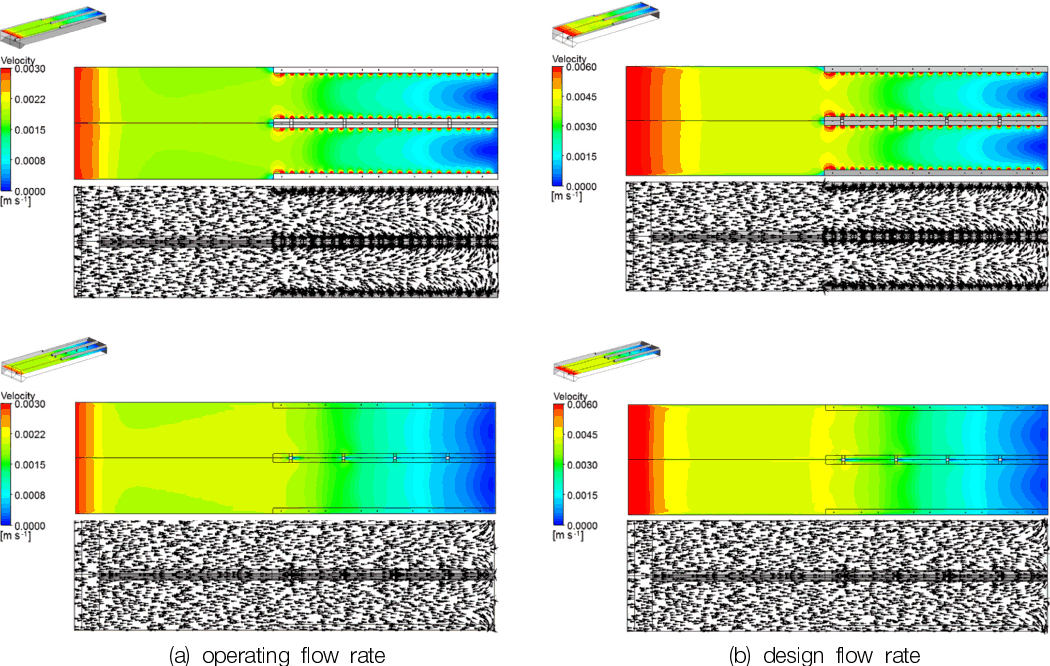
침전효율은 침전지내에서 형성되는 와류, 단략류, 하향류, 상향류 등과 같은 수리적 유동특성에 큰 영향을 받는다. Fig. 5~Fig. 6는 특정한 수직 및 수평면에 대한 침전지 내의 속도분포 및 속도벡터를 결과로서 나타낸 것이다. Fig. 5에서 침전지로 유입되는 물은 유입부 급확대로 속도의 감소가 보이며 이후 트라프로 전단부분까지 일정한 유속 분포가 나타났다.
그러나 유출공이 존재하는 트라프 영역에서는 상승류 흐름이 발생하여 유출부로 물이 빠져나간다. 유출부 흐름은 트라프 시작부분부터 끝단으로 갈수록 유속이 감소하는 것을 볼 수 있다. 입구측에서 설계유량의 속도분포가 상대적으로 빠른 유속영역이 확장된 것을 볼 수 있다. 그리고 운영유량과 설계유량 조건에서는 2배 빠른 유속의 차이를 보였으며, 유동특성은 두 조건에서 모두 유사한 경향을 보였다. Fig. 6을 보면 침전지 입구에서 끝단으로 갈수록 유속은 감소하며 트라프 유출부의 영향으로 유출부에서 빠른 속도 영역이 나타나고 있음을 알 수 있다. 그리고 운영유량과 설계 유량 조건의 유속분포는 유사하게 발생하였으며, 설계유량조건이 운영유량 조건보다 약 2배 많은 유입유량으로 설계유량 조건에서 약 2배 빠른 유속분포가 발생하였다.
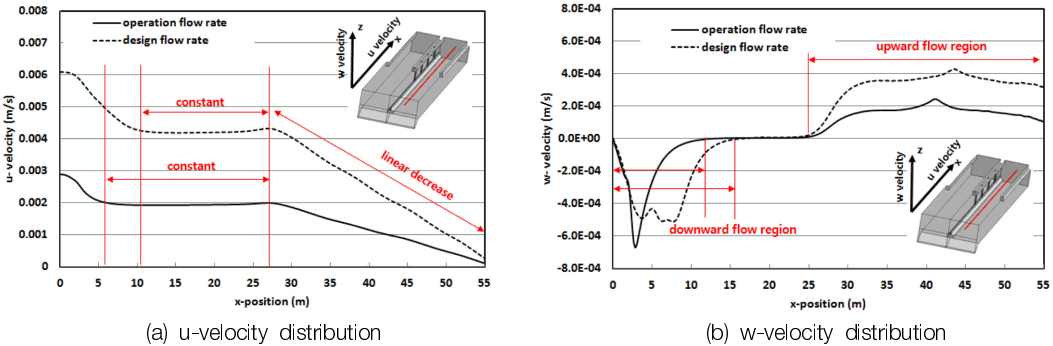
Fig. 7은 침전지내 표시한 선을 따라 유로방향의 속도와 유로방향에 대한 수직방향의 속도값을 나타낸 결과이다. Fig. 7(a)에서 침전지의 유입부에서 유로방향으로 속도는 설계유량 10 m까지, 운영유량 5 m까지 점차적으로 감소하다가 27 m까지는 일정한 속도분포가 나타났다. 27 m 이후 유로방향의 속도는 설계유량과 운영유량조건에 대하여 다시 선형적으로 감소하였다. 설계유량이 운영유량조건에 비해 2배 빠른 속도값을 가지며, 운영유량에 대하여 유사한 속도변화 특징이 나타났다. 그러나 속도가 일정한 부분은 유량이 적은 운영유량조건에서 22 m 영역이 나타났다. Fig. 7(b)에서는 침전지 유입 영역에서는 하강류가 발생하며 운영유량조건 12 m 이후, 설계유량조건 16 m 이후 일정한 속도구배를 갖는 영역이 발생하다가 25 m 이후 설계유량과 운영유량에서 상승류가 발생하였다. 상승류 발생영역에서는 설계유량의 속도가 2배 높은 값을 가진다.
3.2. Tracer Test
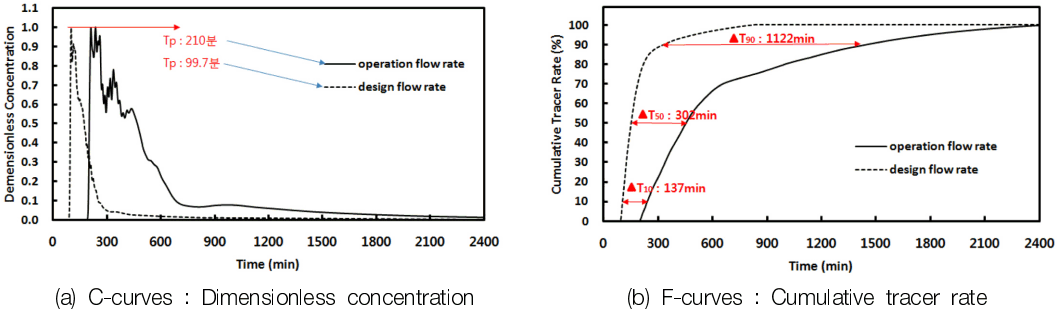
상기 추적자 실험결과를 토대로 각 유출부로 나가는 추적자 농도양상을 이용하여 T10(추적자 양의 10%가 유출되는 시간), T50(추적자 양의 50%가 유출되는 시간), T90(추적자 양의 90%가 유출되는 시간), Tp(최고치의 농도가 유출되는 시간)를 정리한 결과는 Table 3과 같다.
Tracer 모의 결과를 Table 4와 같이 β(유효접촉인자), Morrill Index (T90/T10)와 단락류(Short circuiting) Index ((T50-TP)/T50)로 나타내었으며 운영유량, 시설유량의 β값은 각각 0.51, 0.46으로 나타났다. 운영유량, 시설유량의 Morrill Index값은 각각 6.05와 3.21로 나타났으며, 운영유량, 시설유량의 단락류 Index는 0.54와 0.34로서 일반적으로 침전시 설계에서 요구되는 값을 만족하는 것으로 나타났다.
3.3. 침전지 침전효율
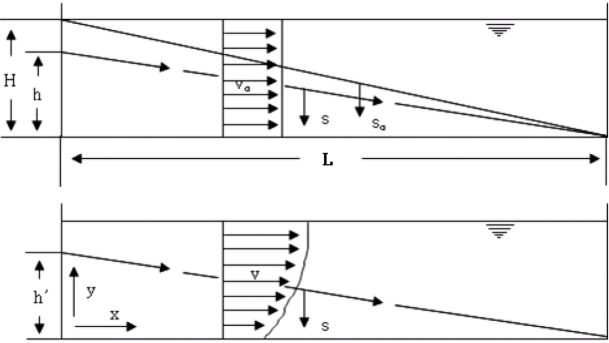
장방형 침전지의 폭과 깊이 전 구간에 걸쳐서 Fig. 9와 같이 수평유속 vo가 일정하다고 한다면, 침전지에 분포되어 있는 모든 부유 입자는 같은 체류시간 To를 가지게 된다. 그러나 실제 침전지에서는 이러한 가정은 현실적이지 못한다. 흐름이 균일하고 어떠한 교란이 없는 조건이라 할지라도 침전지의 벽과 바닥은 no-slip 조건에 의해 마찰력이 작용하게 되므로 벽체 주변의 유속은 침전지 중심부 보다 작아지게 된다.
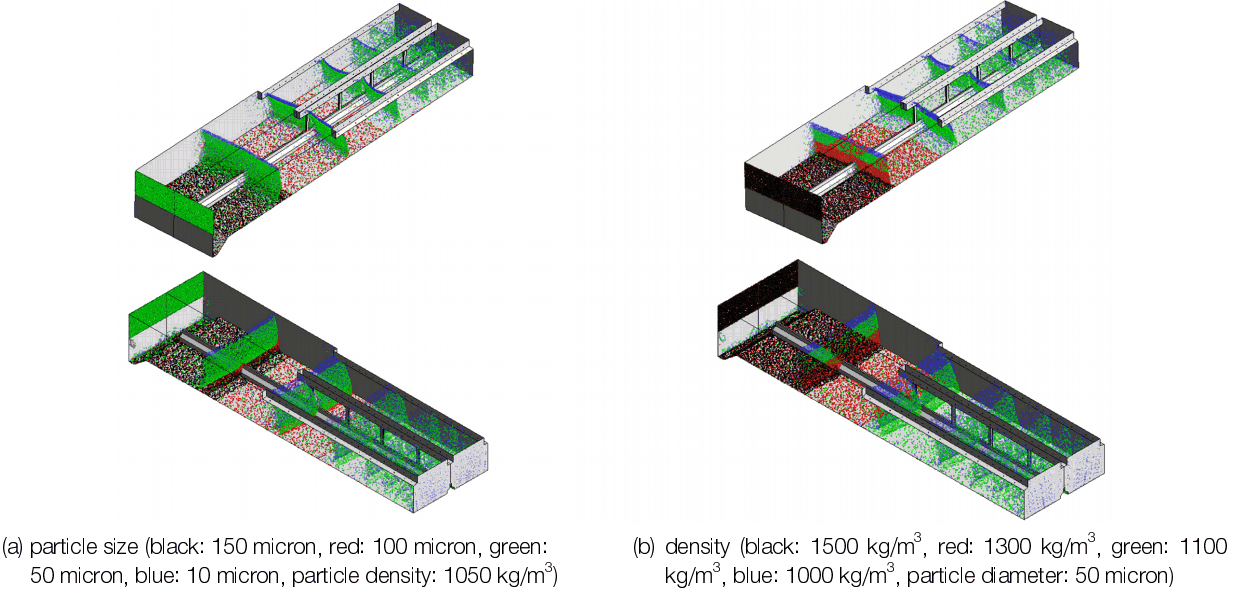
입자의 구성은 플럭의 밀도가 밀정한 경우 크기가 달라질 수 있으며, 플럭의 크기가 일정한 경우 밀도가 달라질 수 있다. 그러므로 플럭의 입자크기, 밀도변화를 고려한 침전효율 예측이 이루어져야 한다. 예로서 Fig. 10은 운영유량 조건에서의 침전지내 입자의 거동을 나타낸 결과이다. Fig. 10(a)는 입자 크기변화에 따른 결과이며, Fig. 10(b)는 입자의 밀도변화에 따른 거동을 나타내고 있다. 침전지를 통해 유입된 특정한 입자의 크기 이상과 특정한 입자의 밀도 이하 값에서 침전지 유출공을 통해 빠져 나가는 것을 거시적으로 알 수 있다.
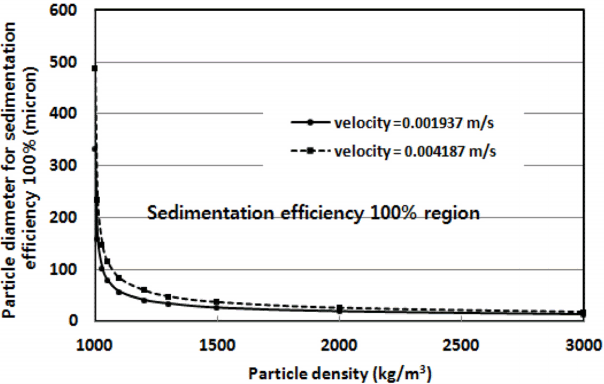
Fig. 9에서 흐름이 존재하는 경우 입자의 침전에 대한 개략도로서 속도 V와 침전 속도 s에 대한 값을 알고 있다면, Fig. 12과 같이 입자에 대한 침전효율이 100%되는 영역과 경계선을 나타낼 수 있다. 본 해석의 침전지 길이 57.3 m에 대하여 Fig. 8의 결과로부터 유로방향으로 속도가 변화하지 않는 plug flow 영역의 속도를 평균화한 값 0.00193 m/s(운영유량)와 0.004187 m/s(시설유량)에 대한 침전 효율 100%일 때의 입자크기 및 입자밀도에 대한 값을 이론적(분석적) 방법으로 도시화 할 수 있다. 입자의 크기가 150 micron보다 작고 밀도가 1100 kg/m3보다 적은 값을 가지는 경우 침전효율의 곡선은 급격하게 변화하며 입자의 크기가 150 micron보다 크고 밀도가 1100 kg/m3보다 큰 경우 침전효율의 곡선은 완만하게 변화하는 것을 볼 수 있다. 그리고 침전지의 평균 유속이 증가할수록 침전효율 곡선은 경향은 유사하나 입자의 크기, 밀도의 값이 이동되는 것을 볼 수 있다.
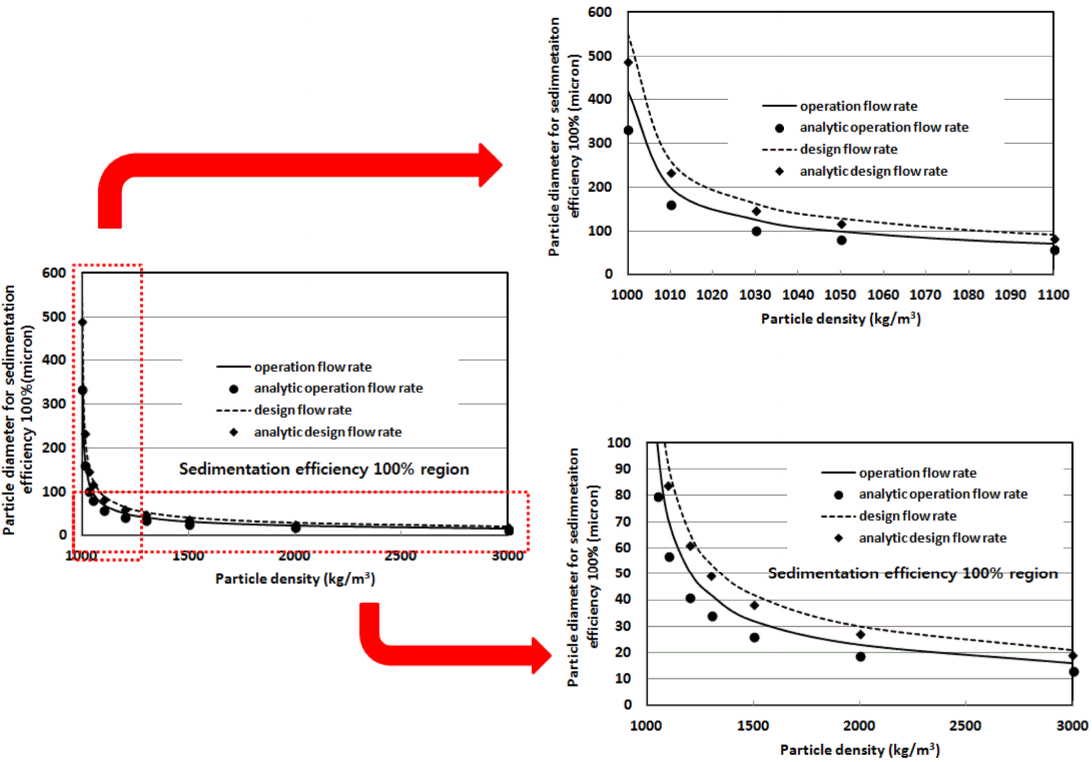
Fig. 12는 침전지 내 다양한 입자 직경, 밀도에 대하여 운영유량과 시설유량 조건으로 CFD 해석과 Stokes 이론을 통한 침전지의 침전 효율 100%되는 경계선을 그래프로 나타낸 결과이다. Stokes 이론적 방법과 CFD 해석을 통한 침전효율곡선은 유사하게 나타났으나 Stokes 이론적 방법을 통한 결과가 상대적으로 낮은 값을 갖는다. 즉 같은 입자 밀도에서 침전 효율 100%를 갖는 입자의 크기는 Stokes 이론적 방법접근이 작은 값을 갖는다.
Table 5는 침전지 내 입자거동에 따른 침전 효율 100%일 경우의 입자 밀도에 따른 입자 크기를 CFD 방법과 Stokes 이론적 방법으로 분석한 정량적 결과로서 이 입자의 크기보다 큰 경우 100%의 침전효율을 나타낸다. CFD 방법은 침전지내의 하강류, 상승류등과 같은 유동특성의 포함하는 경우이며, Stokes 이론적 방법은 침전속도와 plug flow 유동특성만을 고려함으로서 동일 밀도를 가지는 입자에서 침전 효율 100%를 가지는 입자의 크기가 상대적으로 작아지는 것을 알 수 있다.
4. 결 론
본 연구에서는 D_정수장의 침전지를 대상으로 운영유량과 설계유량 조건에서의 수치해석 기법을 사용하여 유동특성과 CFD 해석방법과 Stokes 이론적 방법에 의한 침전효율을 분석하였으며, 다음과 같은 결론을 얻었다.
1) CFD 모사 결과로부터 운영유량과 설계유량 조건에서의 plug flow 영역의 유동특성이 나타나는 속도 값을 구할 수 있으며, 이 영역의 평균 속도값을 0.00193 m/s, 0.00417 m/s로 각각 구할 수 있었다.
2) 운영유량과 설계유량조건의 tracer test 결과 β(유효접촉인자) 값은 각각 0.51, 0.46, Morrill Index값은 각각 6.05와 3.21, 단락류 Index는 0.54와 0.34로 나타났다.
3) CFD 해석방법과 Stokes 이론적 방법으로 도출한 침전효율은 침전지내의 하강류, 상승류등과 같은 유동특성의 영향까지 포함되는 CFD 해석방법이 동일 밀도를 가지는 입자에서 침전 효율 100%를 가지는 입자의 크기가 상대적으로 증가한다. 침전지 설계 시 선행적으로 침전효율까지 고려한 설계가 이루어져야 침전수의 수질향상이 증가할 것으로 판단된다.
4) 향후 CFD 해석기법에 의한 침전효율 경우 입자의 형태를 구형으로 가정하였으므로 다양한 입자의 형상 변화에 대하여 검토가 필요하다.